How To Find The Inverse Of A Rational Function

Finding the Inverse of a Function (page five of 7)

Sections: Definition / Inverting a graph, Is the changed a function?, Finding inverses, Proving inverses

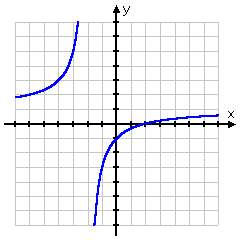
Notice the inverse f(x) = ^{(x � 2)} / _{(x + 2)}, where 10 does non equal �2 .
Is the inverse a role?

First, I recognize that f(10) is a rational function. Here's its graph:

y = (x - 2) / (x + 2)

The restriction on the domain comes from the fact that I can't divide by zero, and then x can't exist equal to �two . I ordinarily wouldn't carp writing downward the restriction, just it's helpful hither because I need to know the domain and range of the inverse. Notation from the picture (and recalling the concept of horizontal asymptotes ) that y will never equal 1 . Then the domain is " x is not equal to �2" and the range is " y is non equal to 1". For the inverse, they'll be swapped: the domain will be " x is not equal to 1" and the range will exist " y is not equal to �2". Here's the algebra:

The original function:
I rename " f(x) " as " y ":
Then I solve for " x =":
Then I solve for " x =":
I go the ten -stuff on one side:
Here'southward the pull a fast one on: I factor out the x !

Then I switch 10 and y :
And rename " y " equally " f -inverse"; the domain restriction comes from the fact that this is a rational function.

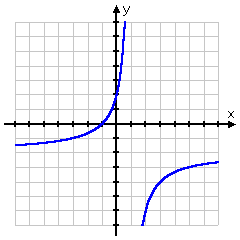
Since the inverse is but a rational function, then the changed is indeed a function.

Hither'southward the graph:

inverse function

Then the changed is y = ^{(�two x � 2)} / _{( x � i)} , and the inverse is also a function, with domain of all 10 non equal to i and range of all y non equal to �two .

Observe the inverse of f(x) = ten ² � iiix + two,x < 1.five

With the domain restriction, the graph looks similar this:

From what I know about graphing quadratics , the vertex is at ( x, y) = (1.five, �0.25) , so this graph is the left-hand "half" of the parabola.

graph of f(x) = x^ii ? 3x + 2, x <= 1.5

The original part:	f(ten) = x ^two � 3x + 2
I rename " f(x) " as " y ":	y = x ² � threex + 2
Now I solve for " ten =" by using the Quadratic Formula :	0 = 10 ² � 3x + 2 � y 0 = x ² � 310 + (2 � y)
Now I solve for " ten =" by using the Quadratic Formula :
Since 10 < 1.5 , and so I desire the negative square root:
Now I switch x and y :
And rename " y " every bit " f -inverse"; the domain restriction comes from the fact that this is a rational function.

Then the inverse is given by:

<< Previous Pinnacle | 1 | ii | three | iv | v | 6 | 7| Return to Index Next >>

Cite this commodity as:

Stapel, Elizabeth. "Finding the Inverse of a Function." Purplemath. Available from
https://world wide web.purplemath.com/modules/invrsfcn5.htm. Accessed